Tìm hiểu về complexity analysis

2020-07-08 Cấu trúc dữ liệu và giải thuật

I, Mở đầu

Hằng ngày, chúng ta phải đối mặt với nhiều vấn đề. Mỗi vấn đề chúng ta có thể nghĩ ra nhiều phương án để giải quyết.
Chúng ta đều mong muốn chọn ra phương án hiệu quả nhất.
Ví dụ như khi đi từ nhà tới nơi làm việc, có thể biết được rất nhiều con đường nhưng chúng ta chỉ muốn đi con đường ngắn nhất để tiết kiệm thời gian và nhiên liệu.
Trong lập trình cũng như thế, khi đối mặt với một vấn đề, các developer cũng sẽ tạo ra các giải thuật khác nhau để giải quyết vấn đề đó.
Điều quan trọng vẫn là tìm ra và sử dụng giải thuật tối ưu nhất.

II, Giải thuật

Ví dụ 1: giải thuật của bài toán tìm tổng của 2 số a và b có thể bao gồm các bước sau:
- Bước 1: Tạo ra biến result để lưu kết quả của a + b.
- Bước 2: Trả về biến result.

fun sun(int a, int b){
    int result = a + b;
    return result;
}

Khi giải quyết 1 vấn đề trong lập trình, chúng ta cần xác định các yếu tố: input, giải thuật và output:
- Input: là dữ liệu đầu vào được xác định từ bài toán. Chúng ta cần chuyển những dữ liệu đầu vào (input) thành kết quả mong muốn (output). Trong ví dụ 1, input là a và b.
- Giải thuật: là tập hợp các bước biến đổi dữ liệu đầu vào (input) thành kết quả mong muốn (output). Trong ví dụ 1, giải thuật gồm 2 bước.
- Output: là kết quả mong muốn của bài toán. Trong ví dụ 1, output là result.
Giải một bài toán trong lập trình tương tự như tạo ra một sản phẩm: từ nguyên liệu thô (input) qua các công đoạn để tạo ra sản phẩm mong muốn (output).
Việc chọn ra giải thuật hiệu quả sẽ giúp tiết kiệm thời gian và tài nguyên của chương trình.
Một giải thuật hiệu quả cần có những yếu tố sau:
- Đúng đắn: với các input đầu vào, giải thuật phải cho ra output đúng theo yêu cầu. Nếu tồn tại ít nhất một output không đúng yêu cầu thì giải thuật đó là sai.
- Giới hạn: đây cũng là 1 yếu tố quan trọng nhưng mọi người thường bỏ qua nó. Giải thuật phải được kết thúc sau một tập các bước xác định. Ví dụ như khi chúng ta tìm kiếm phần tử k trong vòng lặp có n phàn tử, khi tìm thấy phần tử k chúng ta phải dừng tìm kiếm ngay để tránh việc thực thi các thao tác sau không cần thiết.
- Hiệu quả: chúng ta luôn muốn chọn ra giải thuật hiệu quả nhất cho code. Trong lập trình, sự hiệu quả của giải thuật thường được đánh giá bởi hai yếu tố là bộ nhớ và thời gian.

III, Độ phức tạp của giải thuật

Như mình đã nói ở trên, độ hiệu quả của thuật toán phụ thuộc vào hai yếu tố là bộ nhớ và thời gian.
Do đó chúng ta luôn mong muốn tìm ra 1 thuật toán tiêu tốn ít bộ nhớ và thời gian. Nhưng việc này gần như là không thể.
Trong giải thuật, bộ nhớ và thời gian là hai thái cực đối lập với nhau. Nếu giải thuật tiêu tốn ít thời gian thì nó sẽ cần nhiều bộ nhớ và ngược lại.
Hiện nay bộ nhớ gần như không phải là vấn đề để giải quyết vấn đề, do đó người ta thường chú ý nhiều hơn vào yếu tố thời gian.
Mình cũng sẽ đi sâu vào yếu tố thời gian của 1 giải thuật.

1, Bộ nhớ

Mỗi giải thuật cần được cấp 1 lượng bộ nhớ nhất định để hoàn thành.
Ví dụ 2: chúng ta tạo 1 mảng chứa 20 phần tử. Space complexity dựa vào số phần tử của mảng. Nếu số lượng phần tử tăng lên (21, 22…phần tử) thì bộ nhớ yêu cầu sẽ tăng lên.

1	int intArray[] = new int[20]; // allocating memory to array

Trong lập trình, ngay cả khỉ bạn tạo ra 1 object thì chúng ta cũng cần cấp phát bộ nhớ cho nó.

2, Thời gian

Thời gian thực hiện các tác vụ (số thao tác) của 1 giải thuật được phân tích dựa vào kích thước dữ liệu.
Giải thuật hiệu quả nhất là giải thuật có thời gian thực hiện ít nhất.
Chú ý: quy ước rằng mỗi thao tác sẽ có thời gian thực hiện giống nhau.

IV, Phân tích thời gian

Chúng ta sử dụng asymptotic notation để phân tích và dựa vào kích thước của dữ liệu để đưa độ hiệu quả của giải thuật.
Trong phân tích với asymptotic notation, chúng ta xử lý với các kích thước dữ liệu lớn.
Asymptotic notation sẽ chỉ quan tâm tới order of growth của input. Trong order of growth, chúng ta chỉ sử dụng giới hạn lớn nhất vì các giới hạn thấp hơn không đáng kể với kích thước dữ liệu lớn.
Điều này có nghĩa khi chúng ta tăng/giảm kích thước dữ liệu thì thời gian tính của giải thuật sẽ tăng/giảm như thế nào.
Chúng ta có 3 asymptotic notation để mô tả thời gian tính của thuật toán:
- Ω notation (Big omega).
- Θ notation (Big theta).
- Ο notation (Big omicron).
Ví dụ 3: function search() kiểm tra số k có trong mảng arr. Nếu k nằm trong arr thì function sẽ trả về 1, còn không thì sẽ trả về 0. Phân tích bài toán, chúng ta có:
- Input: mảng arr có n phần tử và số k.
- Output: trả về 1 nếu k là 1 phần tử của arr còn không sẽ trả về 0.
- Giải thuật: chúng ta có thể sử dụng linear search được trình bày như sau:

int search(int arr[], int n, int k){
    for(int i = 0, i < n; i++){
        if(arr[i] == k) return 1;
    }
    return 0;
}

Trong function search(), các câu lệnh được thực hiện số lần là:
- i = 0: 1 lần.
- i < n: n + 1 lần.
- i++: n lần.
- arr[i] == k: i lần tuỳ thuộc vào k.
- return 1: nhiều nhất 1 lần.
- return 0: nhiều nhất 1 lần.
Chúng ta có thể nhận ra rằng khi tăng k (thay đổi kích thước dữ liệu) thì thời gian thực hiện giải thuật cũng tăng. Nếu ta có arr[] = [0, 1, 2, 3, 4] thì với:
- k = 0: arr[i] == k thực hiện 1 lần.
- k = 2: arr[i] == k thực hiện 3 lần.
- k >= 4: arr[i] == k thực hiện 5 lần.
Từ đó chúng ta có các khái niệm nói về các trường hợp có thể xảy ra của 1 giải thuật:
- Best case: (trường hợp tốt nhất) trường hợp có thời gian thực hiện giải thuật là ít nhất. Trong ví dụ 3, best case xảy ra khi k = 0.
- Average case: (trường hợp trung gian) chúng ta thử với tất cả input type để tìm ra số lần thực hiện với mỗi kiểu input. Sau đó, chúng ta cộng lại tất cả và chia số kiểu input.
- Worst case (trường hợp tệ nhất) trường hợp có thời gian thực hiện giải thuật là nhiều nhất. Trong ví dụ 3, worst case xảy ra khi k >= 4.

1, Ω notation (Big omega)

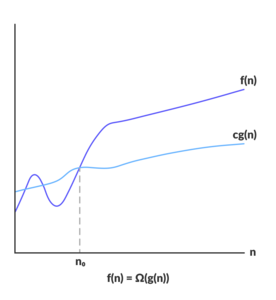
Ω notation nói đến tiệm cận dưới trong giải thuật.
Ω được áp dụng cho best case.

Ω(g(n)) = { f(n) nếu tồn tại các hằng số dương c and n0 sao cho 0 ≤ c.g(n) ≤ f(n) với mọi n ≥ n0 }

Ta nói g(n) là cận dưới tiệm cần của f(n).

2, Θ notation (Big theta)

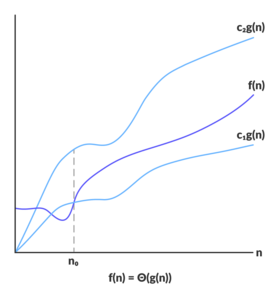
Θ nói đến tiệm cần đúng trong giải thuật.
Θ định nghĩa ra 1 giới hạn trên và giới hạn dưới cho giải thuật.
Ω được áp dụng cho average case.

Θ(g(n)) = { f(n) nếu tồn tại các hằng số dương c1, c2 and n0 sao cho 0 ≤ c1.g(n) ≤ f(n) ≤ c2.g(n) với mọi n ≥ n0 }}

Ta nói g(n) là đánh giá tiệm cận đúng cho f(n).

3, Ο notation (Big omicron)

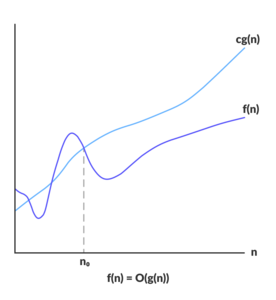
Ο nói đến tiệm cần trên trong giải thuật.
Ο được áp dụng cho worst case.

Ο(g(n)) = { f(n) nếu tồn tại 2 hằng số dương c and n0 sao cho 0 ≤ f(n) ≤ c.g(n) với mọi n ≥ n0 }

Ta nói g(n) là cận trên tiệm cận của f(n).

V, Ví dụ qua bài toán tính tổng

Bài toán:
- Tìm tổng của dãy n phần tử liền kề nhau bắt đầu từ 1 và cách nhau 1 đơn vị. Dãy có dạng là 1, 2, 3, 4..., n-1, n.
- Khi n = 4 thì kết quả là 1 + 2 + 3 + 4 = 10.
- Khi n = 5 thì kết quả là 1 + 2 + 3 + 4 + 5 = 15.
- …

1, Giải pháp Ο(1)

1
2
3

int findSum(int n) {
    return n * (n+1) / 2; // this will take some constant time c1
}

Chúng ta có duy nhất một câu lệnh.
Với mọi kích thước dữ liệu (n = 1, 2, 3…), chúng ta chỉ mất một khoảng thời gian cố định để thực hiện câu lệnh đó.
Do đó chúng ta có thời gian tính của thuật toán trong worst case là Ο(1).

2, Giải pháp Ο(n)

int findSum(int n) {
    int sum = 0;
    for(int i = 1; i <= n; ++i)
        sum = sum + i;
    return sum;
}

Tổng thời gian thực hiện các câu lệnh sum = 0, i = 1 và return sum là c0 (hằng số).
Thời gian thực hiện câu lệnh i <= n là c1 (hằng số). Chúng ta thực hiện n lần i <= n nên tổng thời gian cần để thực hiện c1.n.
Thời gian thực hiện câu lệnh sum = sum + i là c2 (hằng số). Chúng ta thực hiện n lần sum = sum + i nên tổng thời gian cần để thực hiện c2.n.
Tổng thời gian thực hiện các câu lệnh là c1.n + c2.n + c0 hay (c1 + c2).n + c0.
Do đó chúng ta chỉ sử dụng giới hạn lớn nhất nên thời gian tính của thuật toán trong worst case sẽ là Ο(n).

3, Giải pháp Ο(n²)

int findSum(int n) {
    int sum = 0;
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= i; ++j)
            sum++;
    return sum;
}

Tổng thời gian thực hiện các câu lệnh sum = 0, i = 1, j = 1 và return sum là c0 (hằng số).
Thời gian thực hiện câu lệnh i <= n là c1 (hằng số). Chúng ta thực hiện n lần i <= n nên tổng thời gian thực hiên là c1.n.
Thời gian thực hiện câu lệnh j <= i là c2 (hằng số). Chúng ta thực hiện n.(n + 1)/2 lần j <= i do đó tổng thời gian thực hiện là
n.(n + 1)/2.c2.
Tương tự với câu lệnh sum++ thì tổng thời gian thực hiện là n.(n + 1)/2.c3.
Do đó thời gian tính của thuật toán trong worst case là Ο(n²). Mọi người tự tính và lấy giới hạn lớn nhất nhé.

Vũ Đức Sang

Solo leveling

Tìm hiểu về complexity analysis

I, Mở đầu

II, Giải thuật

III, Độ phức tạp của giải thuật

1, Bộ nhớ

2, Thời gian

IV, Phân tích thời gian

1, Ω notation (Big omega)

2, Θ notation (Big theta)

3, Ο notation (Big omicron)

V, Ví dụ qua bài toán tính tổng

1, Giải pháp Ο(1)

2, Giải pháp Ο(n)

3, Giải pháp Ο(n²)